Project Euler #44: A Recursive Golang Solution - Part One
_________________________
 |
| Recursion |
As I studied the Go language, I decided to build a Golang solution for Project Euler #44 - Pentagonal Numbers. A nested for-loop approach, in Go or any other language, would probably work. Then I got a bright idea: maybe I could build a strictly recursive Golang solution instead. Obviously, we should not rely on recursion as a first choice to solve problems. It has a large resource overhead and expense. A recursive solution can become tricky to build, and it can easily blow the stack. However, I wanted to push both myself and the Golang product. I built the solution with Go 1.7.4 and Webstorm 2016.3 on a Windows 7 PC. See the solution here at GitHub.
For Project Euler #44, we have to find two pentagonal numbers that together, obey three rules:
The sum of the numbers must form a pentagonal number
The subtracted value (larger number - smaller number)
form a pentagonal number
The absolute value of the subtracted numbers must be
minimized
The first two rules made perfect sense but I wondered about the third rule. Maybe a later pair of larger numbers might have a smaller distance between them. Then I looked at the pentagonal number

equation. If we start the search from this number pair
P1 = 1
and
P2 = 5
as known pentagonal numbers, I believed that since the equation has a monotonic increasing derivative
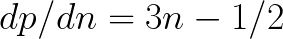
for n > 0, the distance between the numbers in the pairs that solve the problem would always increase. This increase would guarantee that the first detected solution pair satisfies all the rules, especially rule three. Full disclosure: I recently learned that it doesn't work that way. For some later pairs, the distance between the numbers actually decreases. However, the Golang solution discussed here correctly solves the problem. I will discuss the distance issue shortly.
Based on the Pn equation above, the integers "n" map to pentagonal numbers like so:
n pentagonal number (Pn)
____________________________
1 1
2 5
3 12
4 22
5 35
6 51
7 70
8 92
9 117
10 145
. .
. .
. .
To solve the problem, we can start with a pair of integers
(P0, P1)
as shown in the table. Solution pseudo-code would look like this:
(outer loop)
add one to P1
set P0 to (P1 - 1)
(inner nested loop)
with P1 fixed, subtract 1 from P0 until we hit P0 = 1
for each (P0 - 1) calculation, test the (P0, P1) pair
against the rules
For each (P0 - 1) calculation inside the inner loop, map the (P0, P1) pair into pentagonal numbers, and test the pair against the rules. If P0 hits 1 and the (P0, P1) pair did not satisfy those rules, then leave the inner loop, run the outer loop once
add 1 to P1
set P0 to (P1 - 1)
and proceed. The first integer pair that satisfies the rules
P1 is a pentagonal number
P0 is a pentagonal number
(P1 + P0) is a pentagonal number
(P1 - P0) is a pentagonal number
solves the problem. The Project Euler folks probably expected a nested loop solution. After I built the recursive solution that we'll see in Part Two, I found a nested loop solution that someone else built. I modified this solution to find more Project Euler #44 solution pairs, and I placed it here at GitHub. This solution shows the first ten solution pairs, and as shown in the lower comment block, we can see that the behavior becomes almost random. Part Two describes the recursive Golang solution for Project Euler #44.
For Project Euler #44, we have to find two pentagonal numbers that together, obey three rules:
The sum of the numbers must form a pentagonal number
The subtracted value (larger number - smaller number)
form a pentagonal number
The absolute value of the subtracted numbers must be
minimized
The first two rules made perfect sense but I wondered about the third rule. Maybe a later pair of larger numbers might have a smaller distance between them. Then I looked at the pentagonal number

equation. If we start the search from this number pair
P1 = 1
and
P2 = 5
as known pentagonal numbers, I believed that since the equation has a monotonic increasing derivative
for n > 0, the distance between the numbers in the pairs that solve the problem would always increase. This increase would guarantee that the first detected solution pair satisfies all the rules, especially rule three. Full disclosure: I recently learned that it doesn't work that way. For some later pairs, the distance between the numbers actually decreases. However, the Golang solution discussed here correctly solves the problem. I will discuss the distance issue shortly.
Based on the Pn equation above, the integers "n" map to pentagonal numbers like so:
n pentagonal number (Pn)
____________________________
1 1
2 5
3 12
4 22
5 35
6 51
7 70
8 92
9 117
10 145
. .
. .
. .
To solve the problem, we can start with a pair of integers
(P0, P1)
as shown in the table. Solution pseudo-code would look like this:
(outer loop)
add one to P1
set P0 to (P1 - 1)
(inner nested loop)
with P1 fixed, subtract 1 from P0 until we hit P0 = 1
for each (P0 - 1) calculation, test the (P0, P1) pair
against the rules
For each (P0 - 1) calculation inside the inner loop, map the (P0, P1) pair into pentagonal numbers, and test the pair against the rules. If P0 hits 1 and the (P0, P1) pair did not satisfy those rules, then leave the inner loop, run the outer loop once
add 1 to P1
set P0 to (P1 - 1)
and proceed. The first integer pair that satisfies the rules
P1 is a pentagonal number
P0 is a pentagonal number
(P1 + P0) is a pentagonal number
(P1 - P0) is a pentagonal number
solves the problem. The Project Euler folks probably expected a nested loop solution. After I built the recursive solution that we'll see in Part Two, I found a nested loop solution that someone else built. I modified this solution to find more Project Euler #44 solution pairs, and I placed it here at GitHub. This solution shows the first ten solution pairs, and as shown in the lower comment block, we can see that the behavior becomes almost random. Part Two describes the recursive Golang solution for Project Euler #44.