Part Nine - Memory Consumption
Nested C++ Recursion - Introduction (Main Article Page)
Part Eight - Euler 44 Nested Recursion: Classes how C++ classes can increase recursion engineering efficiency. Part Eight here will show how to measure recursive C++ software memory consumption, focusing on the C++ software described in this article.
As business rules change, we can easily add new features to lambdas. In this example, we’ll start with a two-file, integer vector C++ solution to Project Euler #44. We want to add code that measures the stack resources the solution uses. File pentnum_functions.cpp, available in this resource, builds a class called pentnum_functions:
1. #include "stdafx.h"
2. #include "pentnum_functions.h"
3. #include <chrono>
4. #include <ctime>
5. #include <iostream>
6. #include <functional>
7. #include <math.h>
8. #include <vector>
9.
10. pentnum_functions::pentnum_functions()
11. {
12. }
13.
14. bool pentnum_functions::is_pentnum(int x) {
15.
16. float testval = (float)(sqrt(24.0f*(float)(x)+1.0f) + 1.0f) / 6.0f;
17. return (((testval - trunc(testval)) == 0.0) ? true : false);
18. };
19.
20. int pentnum_functions::gen_pentnum(int n) {
21.
22. return (int)(((3 * pow((float)n, 2)) - (float)n) / 2);
23. }
The Euler_44_lambdas.cpp file hosts the main() function:
1. #include "stdafx.h"
2. #include "pentnum_functions.h"
3. #include <chrono>
4. #include <ctime>
5. #include <iostream>
6. #include <functional>
7. #include <math.h>
8. #include <vector>
9.
10. int main() {
11.
12. pentnum_functions pfObj;
13.
14. void *vectorStartPtr;
15. void *vectorPtr;
16.
17. unsigned int frameMaxAddress;
18. unsigned int frameMinAddress;
19.
20. std::function<bool (std::vector<int>&)> innerRecLambda;
21. innerRecLambda = [&innerRecLambda, &pfObj, &vectorPtr, &frameMinAddress](std::vector<int>& x) {
22.
23. bool inner_is_sum_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]));
24. bool inner_is_diff_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]));
25.
26. if ((x[0] > 1) && (!inner_is_sum_pentnum || !inner_is_diff_pentnum)) {
27.
28. x[0]--;
29.
30. return innerRecLambda(x);
31. } else if ((x[0] == 1) && (!inner_is_sum_pentnum || !inner_is_diff_pentnum)) {
32.
33. return false;
34. } else {
35.
36. vectorPtr = (void*)(&(x.begin()));
37. frameMinAddress = *(unsigned int *)(&vectorPtr);
38.
39. return true;
40. }
41. };
42.
43. std::function outerRecLambda;
44. outerRecLambda = [&outerRecLambda, &innerRecLambda, &pfObj](std::vector<int>& x) {
45.
46. bool outer_is_sum_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]));
47. bool outer_is_diff_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]));
48.
49. if (!outer_is_sum_pentnum || !outer_is_diff_pentnum) {
50.
51. x[0] = x[1] - 1;
52.
53. if (!(innerRecLambda(x))) {
54.
55. x[0] = x[1];
56. x[1]++;
57.
58. return outerRecLambda(x);
59. } else {
60.
61. return (x);
62. }
63. } else {
64.
65. return (x);
66. }
67. };
68.
69. std::vector<int> startValues = { 1, 2 };
70. std::vector<int> finishedValues;
71.
72. auto startTime = std::chrono::high_resolution_clock::now();
73.
74. vectorStartPtr = (void*)(&(startValues.begin()));
75. frameMaxAddress = *(unsigned int *)(&vectorStartPtr);
76.
77. finishedValues = outerRecLambda(startValues);
78.
79. auto endTime = std::chrono::high_resolution_clock::now();
80. std::chrono::duration<double> timeDifference = endTime - startTime;
81.
82. std::cout << "\n\tThe calculated x vector values --> pentagonal numbers: " << "\n\n";
83. std::cout << "\tx[1] = " << finishedValues[1] << " --> pfObj.gen_pentnum(x[1]) = pfObj.gen_pentnum(" << finishedValues[1] << ") = " << pfObj.gen_pentnum(finishedValues[1]) << "\n";
84. std::cout << "\tx[0] = " << finishedValues[0] << " --> pfObj.gen_pentnum(x[0]) = pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
85. std::cout << "\t\t\tpfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]) = " << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << "\n";
86. std::cout << "\t\t\tpfObj.gen_pentnum(" << finishedValues[1] << ") + pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
87.
88. std::cout << std::boolalpha;
89.
90. std::cout << "\t\t\t" << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << " is a pentagonal number: " << pfObj.is_pentnum(pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0])) << "\n\n";
91. std::cout << "\t______________________________________________\n";
92. std::cout << "\t______________________________________________\n\n\n";
93. std::cout << "\tx[1] = " << finishedValues[1] << " --> pfObj.gen_pentnum(x[1]) = pfObj.gen_pentnum(" << finishedValues[1] << ") = " << pfObj.gen_pentnum(finishedValues[1]) << "\n";
94. std::cout << "\tx[0] = " << finishedValues[0] << " --> pfObj.gen_pentnum(x[0]) = pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
95. std::cout << "\t\t\tpfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]) = " << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << "\n";
96. std::cout << "\t\t\tpfObj.gen_pentnum(" << finishedValues[1] << ") - pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
97. std::cout << "\t\t\t" << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << " is a pentagonal number: " << pfObj.is_pentnum(pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0])) << "\n\n";
98
99. std::cout << "\n\t\t\tCalculation Time = " << timeDifference.count() << " seconds\n";
100. std::cout << "\n\t\t\tEstimated use of stack resources: " << (frameMaxAddress - frameMinAddress) << " bytes\n\n";
101.
102. system("pause");
103.}
The pentnum_functions class and file match the previous example with no differences. The include of that class in the second Euler_44_lambdas.cpp file at line 2 also matches the previous example, with no differences. Additionally, this class uses integer vectors, as discussed earlier. This example adds code to estimate the stack resource demands of the solution. In Euler_44_lambdas.cpp, lines 14 and 15 declare void pointers, and lines 17 and 18 declare unsigned integer variables. We’ll add code for the new feature to the innerRecLambda lambda, and that code will use these variables. The lambda needs to somehow see most of these variables. Line 21
21. innerRecLambda = [&innerRecLambda, &pfObj, &vectorPtr, &frameMinAddress](std::vector<int>& x) {
adds &vectorPtr and &frameMinAddress to the innerRecLambda closure declaration, to make these variables visible to the innerRecLambda lambda. At line 36, vectorPtr is a void pointer, with the value of the x<int> vector address. For this code, we’ll define x.begin() as the start address of the x<int> vector. innerRecLambda receives the x<int> vector as a parameter. At line 36, the “solution” innerRecLambda stack frame that found the x<int> solution values sets vectorPtr to the x.begin() address of the vector.
That frame also has the largest stack frame address, starting from the stack origin. This happens because the nested recursion calls first placed all the outerRecLambda frames on the stack. Then, the call to innerRecLambda placed the innerRecLambda frames above that. If we measure the x vector address at line 36, we’ll measure it when the software found the solution. At this point, the solution would use the greatest amount of stack resources for both lambdas combined.
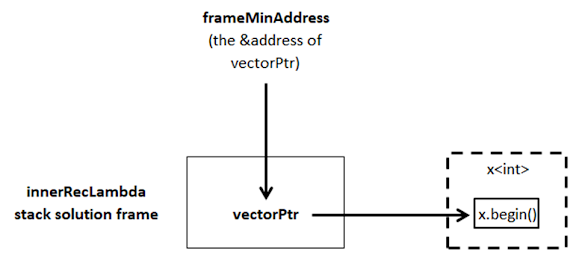
In this block, vectorPtr is a variable, and therefore has its own address. Line 36 converts this address to a void* pointer. The second operation of line 37 – (unsigned int *) – converts it to an integer pointer. Then, line 37 dereferences that integer pointer. This dereference returns the vectorPtr address as an integer, placing that integer value in variable frameMinAddress. This diagram shows how these pointers and dereferences work:
Since this lambda sees frameMinAddress in its lambda closure, the change to the frameMinAddress variable becomes visible outside the lambda – in this case, the entire main() function. We can use the frameMinAddress value later on, to calculate the stack usage.
Lines 74 and 75 make similar calculations to find the address of the startValues vector, before line 77 passes it as an argument to outerRecLambda. The frameMaxAddress and frameMinAddress variable names, and their behavior, might look a little strange. We’ll call the line 75 variable in main() “frameMaxAddress,” and the line 37 variable in innerRecLambda “frameMinAddress,” because technically, a stack fills down, not up.
Here, we explored C++ recursive software memory consumption measurement. In Part Ten - Performance Measures, we'll compare the performance of the recursive solutions described in this article.
Part Eight - Euler 44 Nested Recursion: Classes how C++ classes can increase recursion engineering efficiency. Part Eight here will show how to measure recursive C++ software memory consumption, focusing on the C++ software described in this article.
As business rules change, we can easily add new features to lambdas. In this example, we’ll start with a two-file, integer vector C++ solution to Project Euler #44. We want to add code that measures the stack resources the solution uses. File pentnum_functions.cpp, available in this resource, builds a class called pentnum_functions:
1. #include "stdafx.h"
2. #include "pentnum_functions.h"
3. #include <chrono>
4. #include <ctime>
5. #include <iostream>
6. #include <functional>
7. #include <math.h>
8. #include <vector>
9.
10. pentnum_functions::pentnum_functions()
11. {
12. }
13.
14. bool pentnum_functions::is_pentnum(int x) {
15.
16. float testval = (float)(sqrt(24.0f*(float)(x)+1.0f) + 1.0f) / 6.0f;
17. return (((testval - trunc(testval)) == 0.0) ? true : false);
18. };
19.
20. int pentnum_functions::gen_pentnum(int n) {
21.
22. return (int)(((3 * pow((float)n, 2)) - (float)n) / 2);
23. }
The Euler_44_lambdas.cpp file hosts the main() function:
1. #include "stdafx.h"
2. #include "pentnum_functions.h"
3. #include <chrono>
4. #include <ctime>
5. #include <iostream>
6. #include <functional>
7. #include <math.h>
8. #include <vector>
9.
10. int main() {
11.
12. pentnum_functions pfObj;
13.
14. void *vectorStartPtr;
15. void *vectorPtr;
16.
17. unsigned int frameMaxAddress;
18. unsigned int frameMinAddress;
19.
20. std::function<bool (std::vector<int>&)> innerRecLambda;
21. innerRecLambda = [&innerRecLambda, &pfObj, &vectorPtr, &frameMinAddress](std::vector<int>& x) {
22.
23. bool inner_is_sum_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]));
24. bool inner_is_diff_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]));
25.
26. if ((x[0] > 1) && (!inner_is_sum_pentnum || !inner_is_diff_pentnum)) {
27.
28. x[0]--;
29.
30. return innerRecLambda(x);
31. } else if ((x[0] == 1) && (!inner_is_sum_pentnum || !inner_is_diff_pentnum)) {
32.
33. return false;
34. } else {
35.
36. vectorPtr = (void*)(&(x.begin()));
37. frameMinAddress = *(unsigned int *)(&vectorPtr);
38.
39. return true;
40. }
41. };
42.
43. std::function
44. outerRecLambda = [&outerRecLambda, &innerRecLambda, &pfObj](std::vector<int>& x) {
45.
46. bool outer_is_sum_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]));
47. bool outer_is_diff_pentnum = pfObj.is_pentnum(pfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]));
48.
49. if (!outer_is_sum_pentnum || !outer_is_diff_pentnum) {
50.
51. x[0] = x[1] - 1;
52.
53. if (!(innerRecLambda(x))) {
54.
55. x[0] = x[1];
56. x[1]++;
57.
58. return outerRecLambda(x);
59. } else {
60.
61. return (x);
62. }
63. } else {
64.
65. return (x);
66. }
67. };
68.
69. std::vector<int> startValues = { 1, 2 };
70. std::vector<int> finishedValues;
71.
72. auto startTime = std::chrono::high_resolution_clock::now();
73.
74. vectorStartPtr = (void*)(&(startValues.begin()));
75. frameMaxAddress = *(unsigned int *)(&vectorStartPtr);
76.
77. finishedValues = outerRecLambda(startValues);
78.
79. auto endTime = std::chrono::high_resolution_clock::now();
80. std::chrono::duration<double> timeDifference = endTime - startTime;
81.
82. std::cout << "\n\tThe calculated x vector values --> pentagonal numbers: " << "\n\n";
83. std::cout << "\tx[1] = " << finishedValues[1] << " --> pfObj.gen_pentnum(x[1]) = pfObj.gen_pentnum(" << finishedValues[1] << ") = " << pfObj.gen_pentnum(finishedValues[1]) << "\n";
84. std::cout << "\tx[0] = " << finishedValues[0] << " --> pfObj.gen_pentnum(x[0]) = pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
85. std::cout << "\t\t\tpfObj.gen_pentnum(x[1]) + pfObj.gen_pentnum(x[0]) = " << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << "\n";
86. std::cout << "\t\t\tpfObj.gen_pentnum(" << finishedValues[1] << ") + pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
87.
88. std::cout << std::boolalpha;
89.
90. std::cout << "\t\t\t" << pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0]) << " is a pentagonal number: " << pfObj.is_pentnum(pfObj.gen_pentnum(finishedValues[1]) + pfObj.gen_pentnum(finishedValues[0])) << "\n\n";
91. std::cout << "\t______________________________________________\n";
92. std::cout << "\t______________________________________________\n\n\n";
93. std::cout << "\tx[1] = " << finishedValues[1] << " --> pfObj.gen_pentnum(x[1]) = pfObj.gen_pentnum(" << finishedValues[1] << ") = " << pfObj.gen_pentnum(finishedValues[1]) << "\n";
94. std::cout << "\tx[0] = " << finishedValues[0] << " --> pfObj.gen_pentnum(x[0]) = pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
95. std::cout << "\t\t\tpfObj.gen_pentnum(x[1]) - pfObj.gen_pentnum(x[0]) = " << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << "\n";
96. std::cout << "\t\t\tpfObj.gen_pentnum(" << finishedValues[1] << ") - pfObj.gen_pentnum(" << finishedValues[0] << ") = " << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << "\n\n";
97. std::cout << "\t\t\t" << pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0]) << " is a pentagonal number: " << pfObj.is_pentnum(pfObj.gen_pentnum(finishedValues[1]) - pfObj.gen_pentnum(finishedValues[0])) << "\n\n";
98
99. std::cout << "\n\t\t\tCalculation Time = " << timeDifference.count() << " seconds\n";
100. std::cout << "\n\t\t\tEstimated use of stack resources: " << (frameMaxAddress - frameMinAddress) << " bytes\n\n";
101.
102. system("pause");
103.}
The pentnum_functions class and file match the previous example with no differences. The include of that class in the second Euler_44_lambdas.cpp file at line 2 also matches the previous example, with no differences. Additionally, this class uses integer vectors, as discussed earlier. This example adds code to estimate the stack resource demands of the solution. In Euler_44_lambdas.cpp, lines 14 and 15 declare void pointers, and lines 17 and 18 declare unsigned integer variables. We’ll add code for the new feature to the innerRecLambda lambda, and that code will use these variables. The lambda needs to somehow see most of these variables. Line 21
21. innerRecLambda = [&innerRecLambda, &pfObj, &vectorPtr, &frameMinAddress](std::vector<int>& x) {
adds &vectorPtr and &frameMinAddress to the innerRecLambda closure declaration, to make these variables visible to the innerRecLambda lambda. At line 36, vectorPtr is a void pointer, with the value of the x<int> vector address. For this code, we’ll define x.begin() as the start address of the x<int> vector. innerRecLambda receives the x<int> vector as a parameter. At line 36, the “solution” innerRecLambda stack frame that found the x<int> solution values sets vectorPtr to the x.begin() address of the vector.
That frame also has the largest stack frame address, starting from the stack origin. This happens because the nested recursion calls first placed all the outerRecLambda frames on the stack. Then, the call to innerRecLambda placed the innerRecLambda frames above that. If we measure the x
In this block, vectorPtr is a variable, and therefore has its own address. Line 36 converts this address to a void* pointer. The second operation of line 37 – (unsigned int *) – converts it to an integer pointer. Then, line 37 dereferences that integer pointer. This dereference returns the vectorPtr address as an integer, placing that integer value in variable frameMinAddress. This diagram shows how these pointers and dereferences work:
Since this lambda sees frameMinAddress in its lambda closure, the change to the frameMinAddress variable becomes visible outside the lambda – in this case, the entire main() function. We can use the frameMinAddress value later on, to calculate the stack usage.
Lines 74 and 75 make similar calculations to find the address of the startValues vector, before line 77 passes it as an argument to outerRecLambda. The frameMaxAddress and frameMinAddress variable names, and their behavior, might look a little strange. We’ll call the line 75 variable in main() “frameMaxAddress,” and the line 37 variable in innerRecLambda “frameMinAddress,” because technically, a stack fills down, not up.
Here, we explored C++ recursive software memory consumption measurement. In Part Ten - Performance Measures, we'll compare the performance of the recursive solutions described in this article.